-
Введение
В программу по алгебре и началам анализа экспериментальных классов профильного уровня впервые вошла тема «Элементы комбинаторики, статистики, вероятность». Во всех действующих учебниках для общеобразовательных классов по математике такой темы нет, даже в классах углубленного изучения математики вопросы статистики не изучаются. Учебники по теории вероятности и статистике для вузов не подходят для школьников, т.к. при работе с ними нужны знания выходящие за рамки программы школы , и требуется гораздо больше времени на изучение этого курса, поэтому передо мной стояла задача: отобрать материал из вузовских учебников для изучения курса Теория вероятностей и статистика из расчета 20 часов изучения. Содержание теоретического и практического материала , включенного в это пособие, я старалась изложить в соответствии с требованиями:
1.Отобранный материал должен обеспечивать выполнение обязательного минимума содержания образования для профильных классов.
2.Задачи комбинаторики, теории вероятностей и статистики, включенные в этот курс, призваны познакомить ребят с многообразием вероятностных задач, с методами обработки статистических данных, вызвать у учащихся интерес к дальнейшему изучению этой темы в вузе.
3.Доказательство всех утверждений представляется мне невозможным провести строго из-за недостатка времени и знаний по смежным дисциплинам, поэтому многие вопросы изучаются на конкретных примерах , интуитивно, а затем по аналогии происходит обобщение.
Все задачи, включенные в пособие, приводятся с решениями или ответами. В приложении имеется набор практикумов по нескольким темам курса , самостоятельных и контрольных работ.
Обязательный минимум содержания образования для профильного уровня изучения по теме " Элементы комбинаторики, статистики, вероятность".
Размещения и сочетания. Формулы размещений и сочетаний . Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.
Поле событий. Элементарные и сложные события в классической модели вероятности. Вероятность сложного события. Условная вероятность. Независимые события. Вероятность наступления независимых событий.
Случайная величина.
Дискретные и непрерывные случайные
величины.
Математическое ожидание и дисперсия
случайной величины.
Закон
распределения случайной величины.
Понятие о нормальном распределении
вероятностей.
Требования к уровню подготовки
выпускников по теме.
Изучение темы "Элементы
комбинаторики , статистики , вероятность"
должно предоставить учащимся
возможность :
- усвоить основные формулы
комбинаторики;
- развить представления о классической
модели вероятностей и ее применении;
- получить представления о случайных
величинах и их характеристиках, о
законах распределения случайных
величин.
2. Тематическое
планирование ( 20 часов).
1. Элементы комбинаторики. (5 часов)
1.1 Перестановки , размещения,
сочетания
2 часа
1.2 Размещения и сочетания с
повторениями
1 час
1.3 Формула бинома Ньютона.
Свойства биномиальных
коэффициентов .
Треугольник Паскаля.
2 часа
2. Случайные события .(5 часов)
2.1 Элементарные события.
Сложные события.
2 часа
Определение
вероятности. Теоремы о вероятности.
2.2 Условная вероятность.
Формула Бейеса.
2 часа
2.3 Независимые ,однородные
испытания . Схема
Бернулли.
1 час
3.
Случайные величины. (5 часов)
3.1 Основные понятия.
1 час
3.2 Числовые
характеристики случайной величины.
Свойства математического ожидания,
дисперсии . 3 часа
3.3 Некоторые законы
распределения.
1 час
4. Практикум по решению задач . (
4 часа)
5. Контрольная работа. (1 час)
Список литературы:
1. Введение в теорию вероятностей . Юнита1. Современный гуманитарный университет. Москва, 2001г.
2. Краткий курс теории вероятностей. Юнита4. СГУ, Москва,2000г.
3. Я.К.Колде. Практикум по теории вероятностей и математической статистике.
Москва,"Высшая школа", 1991г.
4. Математика. Факультативный курс, под ред. проф. З.А. Скопеца, М. "Просвещение",1971г.
5. Математика . Самостоятельные и контрольные работы . А.П. Ершова, В.В. Голобородько, Алгебра и начала анализа 10-11 класс, "Илекса",Москва,2002г.
6. Пособие по математике для поступающих в вузы.А.Д.Кутасов и др. М.1981 г.
Практикум
по теме: «Комбинаторика».
Ī вариант 1. Вычислите. ĪĪ вариант
а)
![]() а)
а)
![]()
б)
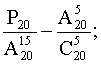 б)
б)
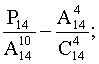
в)
![]() в)
в)
![]()
2. Решите задачу.
Сколькими способами из 7 членов Сколькими способами из 9 учебных президиума собрания можно выбрать предметов можно составить расписание председателя , его заместителя и учебного дня из 6 различных уроков? секретаря?
3. Решите задачу.
Сколькими способами из 10 игроков Сколькими способами из 25 учеников
волейбольной команды можно класса можно выбрать четырех для составить стартовую шестерку? участия в праздничном концерте?
4. Решите уравнение.
![]()
![]()
![]()
![]()
5. Решите задачу.
Сколько диагоналей имеет выпуклый Сколько существует различных семиугольник ? треугольников с вершинами в 7 данных точках , если известно что 3 из них лежат на одной прямой?
6.
![]() Решите задачу.
Решите задачу.
Сколько различных пятизначных Сколько различных трехзначных чисел
чисел можно составить из цифр можно составить из цифр 0,1,2,3,4,
6,7,8,9,0 если цифры в одном числе не
(цифры в одном числе не должны повторяются?
повторяться)?
7. Решите задачу.
Сколько различных перестановок Сколько различных перестановок
можно образовать из букв слова можно образовать из букв слова
«комбинаторика» ? «абракадабра»?
Практикум
по теме «Бином Ньютона».
I вариант. II вариант.
1. Раскройте скобки и упростите
выражение.
а) (х +
![]() )6 ;
а) (х -
)6 ;
а) (х -
![]() )5 ;
)5 ;
б) (2
![]() +
+
![]() )5 .
б) (
)5 .
б) (
![]() - 3
- 3
![]() )4 .
)4 .
2. Найдите показатель степени бинома
(
![]() +
+
![]() )n
, если второй член
(
)n
, если второй член
(
![]() + х)n
, если третий член
+ х)n
, если третий член
разложения не зависит от х. разложения не зависит от х.
3. Найдите член разложения бинома
(
![]() +
+
![]() )n
,
содержащий х в
(
)n
,
содержащий х в
(
![]() +
+
![]() )n
,
содержащий х в
)n
,
содержащий х в
первой степени, если сумма всех первой степени, если сумма всех биномиальных коэффициентов биномиальных коэффициентов
равна 512. равна 128.
4. В разложении бинома
(
![]() +
+
![]() )n
третий биномиальный
(
)n
третий биномиальный
(
![]() +
+
![]() )n
коэффициенты
коэффициент в 4 раза больше второго .
третьего и пятого членов
)n
коэффициенты
коэффициент в 4 раза больше второго .
третьего и пятого членов
Найдите член разложения, относятся как 2:7.
содержащий ![]() Найдите член разложения,
Найдите член разложения,
содержащий ![]() .
.
.
Практикум по теме «Классическая вероятность
I
вариант
II
вариант
1. Бросают две одинаковые монеты. Какова вероятность того, что выпадут,
"орел" и "решка" ? два "орла" ?
2. Из 28 костей домино наугад выбирают
одну. Что вероятнее:
что сумма цифр на ней будет что сумма цифр на ней будет
равна 6
или 8 ?
равна 3 или 4 ?
3.
Какова вероятность того , что ваш
будущий
ребенок
родится:
30
– го числа ?
31- го числа ?
( год не является високосным).
4.
Из букв слова « апельсин »
последовательно выбирают 4 буквы.
Найдите вероятность того , что выбранные
буквы в порядке их выбора
образуют
слово:
«
лиса » ?
« плен » ?
5.
Каждый из трех стрелков стреляет по
мишени
один
раз , причем вероятность попадания 1-го
стрелка
составляет 90%, 2-го – 80 % ,3-го–70 %.
Найдите
вероятность того, что :
а)
все три стрелка поразят
а) все три стрелка
мишень ?
промахнутся ?
б)
двое из трех стрелков
б) двое из трех стрелков
промахнутся ?
поразят мишень ?
Практикум
по теме « Условная и полная вероятность»
I вариант
II
вариант
формулу Бейеса , решите задачи :
Практикум по математической статистике
Выборка:
2
|
4
|
2
|
4
|
3
|
3
|
3
|
2
|
0
|
6
|
1
|
2
|
0
|
2
|
4
|
3
|
2
|
2
|
3
|
3
|
1
|
3
|
3
|
3
|
7
|
4
|
3
|
4
|
2
|
3
|
2
|
3
|
3
|
1
|
4
|
3
|
3
|
6
|
4
|
1
|
3
|
2
|
4
|
1
|
3
|
1
|
0
|
0
|
3
|
2
|
2
|
4
|
3
|
3
|
5
|
1
|
1
|
1
|
2
|
3
|
1
|
4
|
3
|
1
|
1
|
4
|
5
|
3
|
4
|
2
|
4
|
5
|
4
|
6
|
4
|
7
|
4
|
1
|
3
|
|
|
|
|
|
По данной выборке составить:
| вариационный ряд; | |
| вычислить относительные и накопленные частости; | |
| построить полигон и гистограмму; | |
| составить эмпирическую функцию распределения; | |
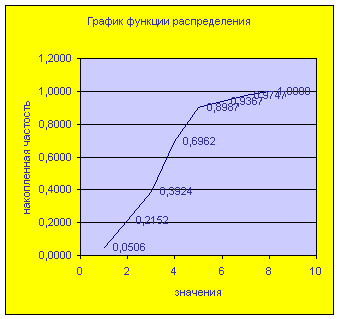
| построить график эмпирической функции распределения; | |
| вычислить числовые характеристики вариационного ряда: |
- выборочное среднее;
- выборочную дисперсию;
- среднеквадратическое отклонение;
- моду;
-
медиану.
Пример выполнения:
|
значение случайной величины |
частота появления |
относительная частость |
накопленная частость |
|
0 |
4 |
0,0506 |
0,0506 |
|
1 |
13 |
0,1646 |
0,2152 |
|
2 |
14 |
0,1772 |
0,3924 |
|
3 |
24 |
0,3038 |
0,6962 |
|
4 |
16 |
0,2025 |
0,8987 |
|
5 |
3 |
0,0380 |
0,9367 |
|
6 |
3 |
0,0380 |
0,9747 |
|
7 |
2 |
0,0253 |
1,0000 |
|
сумма |
79 |
1,0000 |
|