







Элементы теории вероятностей.
Теория вероятностей – математическая
наука , изучающая закономерности в
случайных явлениях.
1. Случайные события.
Основные понятия.
Р Рассмотрим простой опыт , заключающийся в подбрасывании монеты. Этот опыт имеет два исхода : либо монета упадет так , что сверху окажется герб, либо она ляжт ляжет гербом вниз. Тот или иной исход опыта зависит от многих причин , которые не пнне поддаются учету , и заранее предсказать результат опыта нельзя. Событие ,состсостоящее в том , что ’’выпал герб’’ , является примером случайного события. ДругДругими примерами случайных событий могут служить : появление единицы при бросбросании игрального кубика , выход из строя электролампы до определенного сроксрока и т.д.
Резу Результат некоторого опыта или наблюдения будем называть событием.
Эле Элементарным исходом будем называть элементарное , неразложимое
соб событие.
Соб События называются элементарными , если они обладают свойствами:
- - взаимно исключают друг друга , и в результате опыта обязательно происходит одно из этих элементарных событий;
- каково бы ни было случайное событие А ,по наступившему элементарному событию можно сказать о том , произошло или не произошло событие А
Элементарные события обычно обозначаются греческими буквами ,а их в совокупность - Ώ будем называть пространством элементарных событий.
Пример. При бросании игрального кубика элементарными событиями можно
считать появление любого числа от 1 до 6. Очевидно ,что в этом опыте всего им имеется 6 элементарных событий.
- Алгебра событий.
Событие называется достоверным , если оно наступает в результате любого
элементарного события. Обозначается достоверное событие Ώ (омега).
Пример: при бросании кубика выпадет натуральное число , меньшее 7. Это
достоверное событие.
Невозможным называется событие, не наступающее ни при каком
элементарном
событии. Невозможное событие обозначается символом Ǿ . Пример: в опыте с
кубиком выпадет отрицательное число.
Суммой двух событий А и В назовем событие А+В или (АƯВ), происходящее
тогда и только тогда, когда происходит или А , или В.
Пример:Событие « выпало четное число» является суммой событий : выпало
2,выпало 4, выпало 6.
Очевидные соотношения :
А+ Ǿ=А ; А+ Ώ= Ώ ; А+А=А .
Произведением событий А и В назовем событие АВ или (А∩В), которое
происходит тогда и только тогда , когда происходит и А ,и В.
Пример: при бросании игрального кубика «выпало 5» является произведением событий : выпало нечетное и выпало больше трех. Очевидно соотношение:
А Ǿ= Ǿ ; А Ώ=А ; АА=А .
Два события назовем несовместимыми, если их одновременное появление в опыте невозможно , т.е. АВ= Ǿ.
ПРИМЕР: Выпало четное и нечетное число при бросании игрального кубика – события несовместимые.
Событие
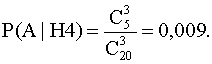 назовем противоположным к событию
назовем противоположным к событию
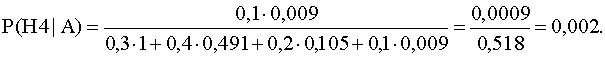 , если оно происходит
тогда и только тогда
,когда не
происходит событие
, если оно происходит
тогда и только тогда
,когда не
происходит событие
![]() .Очевидно соотношение:
.Очевидно соотношение:
![]() +
+
![]() =
=
![]() ;
А
;
А
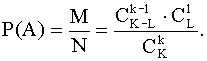 = Ǿ ;
= Ǿ ;
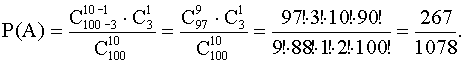 = А .
= А .
ПРИМЕР: Выпало четное и нечетное число (при бросании одного игрального кубика) - события противоположные.
Разностью событий A
и B
назовем событие
A\ B , происходящее
тогда и только тогда
,когда происходит
событие
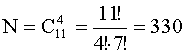 ,но не
происходит событие тогда и только тогда
,когда не
происходит событие В.
Очевидные соотношения:
,но не
происходит событие тогда и только тогда
,когда не
происходит событие В.
Очевидные соотношения:
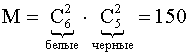 .
.
ПРИМЕР 1 . Производится два выстрела по цели . Пусть событие A - попадание в цель при первом выстреле , В – при втором , тогда:
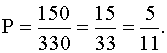 – промах при
первом выстреле;
– промах при
первом выстреле;
![]() - промах при
втором выстреле.
- промах при
втором выстреле.
Пусть поражение цели событие С (когда достаточно хотя бы одного попадания)
выразим через А и В.
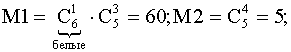 -
попадание при двух выстрелах;
-
попадание при двух выстрелах;
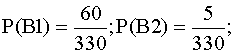 – промах при
первом выстреле и попадание при втором;
– промах при
первом выстреле и попадание при втором;
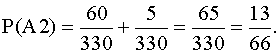 – попадание при
первом и промах при втором. Тогда :
– попадание при
первом и промах при втором. Тогда :
С=
А
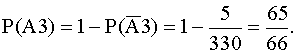 +
+
![]() В + АВ.
В + АВ.
С другой стороны :
С =
![]() -
событие ,противоположное двум промахам.
-
событие ,противоположное двум промахам.
ПРИМЕР 2. Бросание монеты .Пусть монета подбрасывается три раза . Обозначим Г –выпадание герба при одном бросании, Р- решки . Пространство элементарных исходов состоит из 8 точек:
ГГГ ГГР ГРГ РГГ ГРР РГР РРГ РРР.
Событие А «Выпало не менее двух гербов» это : ГГГ ГГР ГРГ РГГ.
Событие В « Выпало ровно одна решка» означает : ГГР ГРГ РГГ.
3. Определения вероятности.
Классическое определение вероятности события формулируются следующим образом:
Вероятность Р( А) события А равна отношению числа возможных результатов опыта (М) ,благоприятствующих событию А , к числу всех возможных результатов опыта (N) :
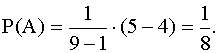
Примеры вычисления вероятности по классической формуле :
Пример 1.Подбрасывание игральной кости один раз.
Событие А – «Выпавшее число очков- четно». В этом случае N=6 – число граней куба, М= 3 – число граней с четными номерами. Тогда Р(А)= 3: 6= 0,5.
Пример 2.Подбрасывание монеты два раза.
Событие А- «Выпало ровно два герба» . В этом случае N=4 (ГГ ГР РГ РР ), М=1,т.к. А=ГГ .
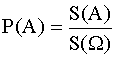
Пример 3.Вытягивание шара из урны , содержащей 2 белых и 3 черных шара .
Событие А- «Вытянули черный шар». N= 2+3=5 ( всего шаров в урне), М=3 ( число черных шаров).
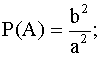
Пример 4.Набирая номер телефона абонент забыл две последние цифры. Какова вероятность того , что он с первого раза наберет эти цифры правильно, если он помнит ,что они различны ?
Решение: Событие А- «Две последние цифры набраны правильно».
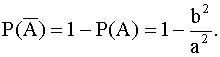
М=1
(Один вариант верный )
![]() .
.
Пример 5.В урне 3 белых и 4 черных шара. Из урны вынимают два шара. Найти вероятность того ,что оба шара будут белыми.
РЕШЕНИЕ: Обозначим событие А – «Вынули 2 белых шара».
![]() (Всего
вариантов)
(Всего
вариантов)
![]() (Благоприятных
вариантов)
(Благоприятных
вариантов)
![]() .
.
4.СВОЙСТВА ВЕРОЯТНОСТИ.
Вероятность любого события А удовлетворяет неравенствам .
![]()
Т,к. в формуле классической
вероятности
![]() .
.
Вероятность достоверного события
равна
![]() .
.
Вероятность невозможного события равна Р( Ǿ )=0.
Вероятность суммы событий равна А+В равна Р(А+В) = Р(А) + Р(В) – Р(АВ) ;
Если события А и В несовместимы ,то формула суммы двух событий упрощается
Р(А + В) = Р(А) + Р(В).
С помощью этой формулы можно найти вероятность противоположных событий:
А +
![]() =
Ω , Р(А +
=
Ω , Р(А +
![]() ) = Р( Ω) , Р(А) +
Р(
) = Р( Ω) , Р(А) +
Р(
![]() ) = 1 , Р(
) = 1 , Р(
![]() ) = 1–Р(А).
) = 1–Р(А).
События называются независимыми , если происхождение одного события не зависит от того произошло ли другое событие или нет.
При зависимых событиях А и В имеет смысл говорить об условной вероятности (Р(А|В)) события А при условии ,что событие В уже произошло.
![]() При
независимых событиях
Р(А| В) =Р(А).
При
независимых событиях
Р(А| В) =Р(А).
Вероятность произведения
событий АВ выражается
формулой P(AB) = P(A|B)·P(B)
![]() или Р(АВ) =Р(А
В)·Р(В).
или Р(АВ) =Р(А
В)·Р(В).
ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ СВОЙСТВ ВЕРОЯТНОСТИ ПРИ РЕШЕНИИ ЗАДАЧ.
Прибор , работающий в течении время t , состоит из трех узлов ,каждый из которых , независим от других, может выйти из строя в течении времени t.отказ хотя бы одного узла приводит к отказу прибора в целом. За время t Надежность (вероятность безотказной работы) первого узла 0,9 ; второго узла 0,8 ,а третьего – 0,7. Найдите надежность прибора в целом ?
РЕШЕНИЕ: А – безотказная работа прибора;
А1 – безотказная работа 1 узла ;
А2 – безотказная работа 2 узла ;
А3 - безотказная работа 3 узла ;
А= А1·А2·А3; А1,А2,А3 – независимые события.
Р(А)=р(А1·А2·А3)=
Р(А1) ·Р(А2) ·Р(А3)= О,9·0,8·0,7=О,504.
Студент пришел сдавать зачет, зная из 30 вопросов только20. Какова вероятность сдать зачет ,если после отказа отвечать на первый вопрос преподаватель задает еще один ?
РЕШЕНИЕ:
А – студент сдаст зачет ;
В – студент ответил на первый вопрос ;
С – студент ответил на второй вопрос .
А
= В +
![]() ·С , т.е. студент сдаст зачет ,если он
ответит на первый вопрос или , не ответив
на первый , ответит
на второй .
·С , т.е. студент сдаст зачет ,если он
ответит на первый вопрос или , не ответив
на первый , ответит
на второй .
Р(А)
= Р(В +
![]() С) = Р(В) + Р(
С) = Р(В) + Р(
![]() С) – Р(В
С) – Р(В
![]() С)
С)
В
![]() С = Ǿ , т.к. В
и
С = Ǿ , т.к. В
и
![]() не могут
выполняться одновременно, значит :
Р(А)
= Р(В) + Р(
не могут
выполняться одновременно, значит :
Р(А)
= Р(В) + Р(
![]() С);
С);
Р(В)
=
![]() ;
Р(С
;
Р(С
![]() ) = Р(С |
) = Р(С |
![]() ) · Р(
) · Р(
![]() ).
).
Р(
![]() ) = 1 – Р(В) =
) = 1 – Р(В) =
![]() ;
Р(С|
;
Р(С|
![]() ) =
) =
![]() ,т.к.
осталось 29 вопросов ,из них студент
знает 20.
,т.к.
осталось 29 вопросов ,из них студент
знает 20.
Р(А)
=2/3 + 20/29*1/3 = 26/29
3. Вероятность попадания в цель первым стрелком равна 0,8 ; а вторым 0,7. Стрелки делают по цели по одному выстрелу одновременно. Определить вероятность того , что цель будет поражена ,если стрелки стреляют не зависимо друг от друга.
РЕШЕНИЕ:
1 Способ.
А1 – цель поражена первым стрелком ;
А2 – цель поражена вторым стрелком ;
А – цель поражена .
А = А1 + А2. по правилу сложения :
Р(А)
= Р(А1 + А2) = Р(А1) + Р(А2) – Р(А1А2) = 0,8 + 0,7 – 0,8 ·
0,7 = 0,94.
2 СПОСОБ.
![]() – цель
поражена .
– цель
поражена .
А
![]() =
=
![]() 1 *
1 *
![]() 2
2
Р(
![]() ) = Р(
) = Р(
![]() 1·
1·
![]() 2) = Р(
2) = Р(
![]() 1) · Р(
1) · Р(
![]() 2) = (1 – 0,8) · (1 – 0,7) = 0,06.
2) = (1 – 0,8) · (1 – 0,7) = 0,06.
Р(А) = 1 – Р(
![]() ) = 1 – 0,06 = 0,94.
) = 1 – 0,06 = 0,94.
6 ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ.
Пусть требуется определить вероятность некоторого события А , которое может произойти вместе с одним из событий Н1 ,Н2,Н3,…,НN, которые являются несовместимыми. Эти события будут называться гипотезами. В этом случае вероятность события А вычисляется как сумма произведений вероятности каждой гипотезы на условную вероятность событий при этой гипотезе :
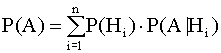
Эта формула называется формулой полной вероятности.
ПРИМЕРЫ: Имеются 3 одинаковые на вид урны: в первой урне 2 белых и 1 черный шар ; во второй урне 3 белых и 1 черный; в третьей – 2 белых и 2 черных шара. Некто выбирает наудачу одну из урн и выбирает из нее шар. Найти вероятность того, что этот шар - белый.
РЕШЕНИЕ : Рассмотрим три гипотезы :
Н1 – выбрана 1 урна;
Н2 – выбрана 2 урна ;
Н3 – выбрана 3 урна .
Р (Н1) = Р (Н2) = Р (Н3) =
![]()
Условные вероятности события А при этих гипотезах :
Р (А |
Н1) =
![]() ;
Р (А | Н2) =
;
Р (А | Н2) =
![]() ;
Р (А|Н3 ) =
;
Р (А|Н3 ) =
![]() ;
;
Р (А) =
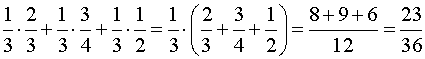 .
.
2. Пластмассовые изделия изготавливаются на трех прессах . Первый пресс вырабатывает – 50% всех изделий , второй – 30 % и третий – 20 %.
При этом первый пресс дает 0,025 % брака , второй - 0,02 % , а третий – 0,015 %.
Найдите вероятность того , что наугад взятое со склада изделие соответствует стандарту.
РЕШЕНИЕ:
Н1 – появление изделий с 1 пресса ;
Н2 – появление изделий со 2 пресса ;
Н3 – появление изделий с 3 пресса.
А – соответствует стандарту.
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]()
- Некто вышел из дома и не может вспомнить ,какая улица ведет к его школе Он выбирает наугад один из возможных путей ( см. рисунок). Какова вероятность того , что он при этом попадет в школу ?



![]()
Решение: обозначим Нi – выбор дороги.
![]()
Событие D – путник добрался до школы
![]()
![]()
![]()
![]()
7 . Формула Бейеса. |
Если событие А произошло ,то можно вычислить условную вероятность того, что
вместе с событием А осуществилась гипотеза Нi.
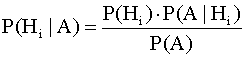
Примеры использования формулы Бейеса.
1. На предприятии изготавливаются изделия определенного вида на трех
поточных
линиях. На 1 линии производится 20% изделий от всего объема их производства, на 2 – 30% , на 3 – 50%. Каждая линия характеризуется соответственно
следующими процентами брака: 5%, 2%, 3;. Наугад взятое изделие оказалось
бракованным. Какова вероятность того , что оно сделано на первой линии?
Решение:
Нi – изделие произведено на i-той линии.
![]()
![]()
![]()
А – изделие оказалось бракованным.
![]()
![]()
![]()
По формуле Бейеса:
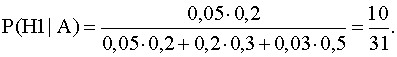
3. В группе из 10 студентов ,пришедших на экзамен, 3 подготовлены отлично, 4 –
хорошо, 2 – удовлетворительно и 1 – плохою Имеется 20 вопросов , причем :
отлично подготовленный студент может ответить на все вопросы , хорошо
подготовленный – на 16 , удовлетворительно подготовленный – на 10 и плохо
подготовленный – на 5.
Вызванный наугад студент , ответил на три заданных ему случайным образом
вопроса. Найти вероятность того , что этот студент плохо подготовлен и ему
просто повезло с вопросами.
Решение:
А – случайно выбранный студент ответил на все доставшиеся ему вопросы.
Н1 – студент подготовлен отлично,
![]()
Н2 – студент подготовлен хорошо,
![]()
Н3 – студент подготовлен
удовлетворительно,
![]()
![]()
Н4 – студент плохо подготовлен,
![]() .
.
P(A|H1) =1; P(A|H2) =
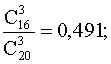
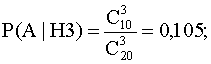
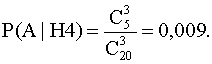
По формуле Бейеса:
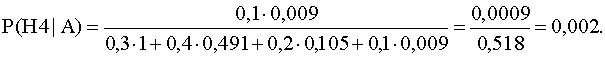
8.
Задача «контроля качества».
Среди K поставленных единиц товара n не удовлетворяет предъявленным
условиям . Найти вероятность того ,что
среди k
![]() K ,
отобранных для
K ,
отобранных для
выборочного контроля качества , ровно
l
![]() L не
будут удовлетворять этим требованиям.
L не
будут удовлетворять этим требованиям.
Решение: опыт заключается в случайном отборе k образцов. Следовательно ,
исходы этого испытания равновозможны и
их общее число равно
![]() .
.
Событие А состоит в том , что из k отобранных ровно l будут удовлетворять
этим требованиям. Число исходов , благоприятствующих А , согласно правилу
произведения
![]() -
-
здесь первый множитель дает число вариантов отбора хороших , а второй
плохих образцов.
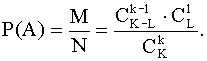
Задача1. В партии товара из 100 электрических ламп 3% бракованных. Найти
вероятность
того, что в коробке из 10 ламп окажется ровно одна бракованная.
Здесь К=100;
L= 100 · 0,03=3; |
К=10; l = 1.
А – ровно одна бракованная.
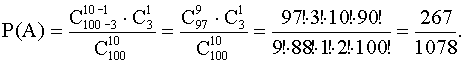
Задача2. В урне 5 черных и 6 белых шаров. Случайным образом вынимают 4
шара. Найти вероятность того , что среди них найдется:
а) 2 белых шара;
б ) меньше , чем 2 белых шара;
в) хотя бы один белый шар.
Решение:
Всего исходов
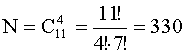
а) число
благоприятных исходов :
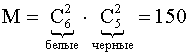
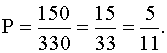
б) А2 – событие «среди вынутых шаров меньше, чем 2 белых»
(т.е. в1 – один белый и 3 черных или в2 – нет ни одного белого)
![]()
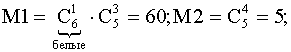
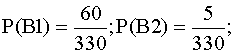
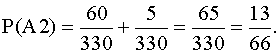
в) A3- среди вынутых шаров хотя бы один белый.
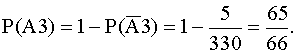
9.
Геометрическая схема вероятности.
Рассмотрим отрезок [0;m].
Бросаем на этот отрезок точку случайным образом ( попадания в любую
точку равновозможны).
Событие А – попадание точки на отрезок [ a ; b ], входящий в отрезок [ o ; m ].
Решение: P( A ) = k ( b – a ) – вероятность пропорциональна длине отрезка.
- достоверное событие попадания на отрезок [ o ; m ],
P ( Ω ) =
1 = k ( m – o
)
k =
![]() ;
P (A) =
;
P (A) =
![]() ·
(b – a ).
·
(b – a ).
Задача. Случайное событие – вероятность
падения в
промежуток [4
; 5] точки ,
брошенной на отрезок
[1 ; 9].
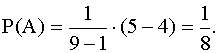
Аналогично для плоской фигуры.
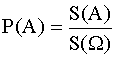 , где
S(Ω) и S(A)
- площади соответствующих
фигур.
, где
S(Ω) и S(A)
- площади соответствующих
фигур.
Задача. В квадратном окне со стороной а есть квадратная форточка со
стороной в .Во время игры мяч случайно попадает в окно. Какова вероятность
,что окно при этом : а) не разобьется;
б) разобьется ?
Решение:
а)
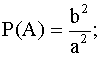
б)
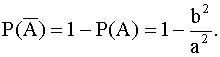
10. Повторные испытания. Схема
Бернулли.
Предположим, что событие А происходит в результате n независимых испытаний
, притом в каждом испытании вероятность события А постоянна и равна Р.
Результатом каждого испытания является
либо событие А ,либо событие
![]() .
.
Последнее происходит с вероятностью q=1 – р.
Если рассматривать все n испытаний как одно испытание , то его результатом
является произведение вероятностей
событий А и
![]() . Здесь ввиду
. Здесь ввиду
независимости исходных испытаний важен не порядок событий, а число
повторений события А. Частоту повторения события А обозначим k ,
(0
![]() k
k
![]() n). Вероятность появления события А
k раз
вычисляют
n). Вероятность появления события А
k раз
вычисляют
по формуле
Бернулли:
![]() где
где
![]()
Задача1. Всхожесть семян данного сорта растений оценивается вероятностью 0,8. Какова вероятность того, что из 5 посеянных зерен взойдет не меньше 4 ?
Решение:
![]()
Задача2. Вероятность того, что образец бетона выдержит нормативную нагрузку ,
равна 0,9. Найти вероятность того, что из 7 образцов испытания выдержат:
а) ровно 5; б) не менее 5.
Решение:
а)
![]()
б)
![]()