Случайные величины.

1.      Основные понятия.

         Одним из основных понятий теории вероятностей является понятие случайной величины. Число отличных отметок на экзамене, число ничейных результатов в шахматном турнире, расстояние точки падения диска от точки метания, вес наугад взятого зерна пшеницы, число избирателей, которые могут отдать голоса определенному политическому блоку, - примеры случайных величин, относящихся к различным областям жизни.

         Случайной величиной называется переменная величина, значения которой зависят от случая. Пусть Х – случайная величина, х – действительное число. Вероятность того, что Х примет значение, меньшее, чем х, называется функцией распределения вероятностей случайной величины: F_х (х) = р(Х<х).

Дискретные случайные величины – это случайные величины, которые могут принимать только конечное или счетное (бесконечное множество, все элементы которого можно занумеровать натуральными числами) множество значений.

 Примеры:

-         число появлений герба при трех бросаниях монеты ( возможные значения 0,1,2,3);

-         число выстрелов в цель до первого попадания  (возможные значения 1,2,…,N, где N-число имеющихся в наличии патронов);

-         число опечаток в книге.

Непрерывные случайные величины – это величины, возможные значения которых образуют некоторый конечный или бесконечный интервал.

Примеры:

-         интервал между поездами метро 2 мин. Человек попадает на платформу в случайный момент времени. Время ожидания поезда х [0;2];

-         длительность безаварийной работы различных машин и приборов;

-         случайное отклонение при затаривании мешков с сахаром;

-         урожай с одной сотки.

Свойства функции распределения дискретной случайной величины: F_х (х) = р(Х<х).

1)      F_х (х) –неубывающая функция. Это следует из определения функции распределения.

2)      F_х (- ) = 0 ; F_х (+ ) = 1.

3)      F_х (х) = р(Х<х) = .

Пример. Абитуриент сдает два вступительных экзамена:  по физике и математике. Составить закон распределения случайной величины Х числа полученных пятерок, если вероятность получения пятерки по математике равна 0,8, а по физике – 0,6.

Решение:

Возможные значения случайной величины Х есть 0,1,2, причем

Р(х=0) = 0,2·0,4 = 0,08,

Р(х=1) = 0,8·0,4 + 0,2·0,6 = 0,44,

Р(х=2) = 0,8·0,6 = 0,48.

F(х) =  

                           2. Числовые характеристики случайной величины.

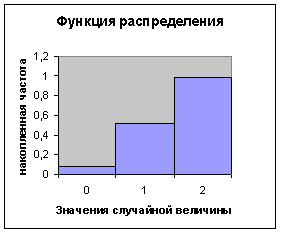
    Математическим ожиданием дискретной случайной величины Х назовем сумму произведений всех ее возможных значений на их вероятности.

                                           М(х) = а =

Вернемся к предыдущему примеру.

М(х) = 0·0,08 + 1·0,44 + 2·0,48 = 1,4

Количество пятерок из двух экзаменов вероятно 1,4.

                           Свойства математического ожидания.

1. Математическое ожидание постоянной равно самой постоянной. М(С)=С.

Это следует из того, что случайная величина принимает единственное значение С=const  c вероятностью 1.

2. Постоянный множитель можно выносить за знак математического ожидания:

             М(Сх)= С·М(х).

      Это следует из того, что при умножении на С возможные значения случайной

     величины также умножаются на С , при сохранении соответствующих    

           вероятностей.

3. Математическое ожидание суммы случайных величин равно сумме   

      математических ожиданий слагаемых ( приводится без обоснования).

        Дисперсией случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

          D(х) = М((х-а)²)   или  D(х)  = .

Для практических расчетов чаще применяют другую формулу.

D(х) = М((х-а))² = М(х² –2ах+а²) = М(х²) – М(2ах) + М(а²) = М(х²)  –2а·М(х) + а² =

=М(х²) –2а² + а²  = М(х²) -  а²  = М(х²) – (М(х))².

                                        Свойства дисперсии.

1. Дисперсия постоянной равна 0.  D(С) = 0,т.к. D(С) = М(С²) – (М(С))² = С² - С²  =0.
2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат, т.е. D(Сх) = С² · D(х).

           Доказательство:

 D(Сх) = М(С²х²) – (М(Сх))²   = С² М(х²) – С² (М(х))²  = С²  ·( М(х²) – (М(х))²) = С² · D(х).

3. Дисперсия суммы равна сумме дисперсий слагаемых.

       D(X+Y ) = D(X)+ D(Y) (без обоснования).

Среднеквадратическим отклонением называют (х) = .

Итак: математическое ожидание является тем «средним» значением, вокруг которого распределены все возможные значения случайной величины. Случайные величины при одинаковом среднем могут меняться в узких пределах или в широких. Для того, чтобы охарактеризовать разброс, рассеяние случайной величины применяют дисперсию или среднеквадратическое отклонение .

Задачи . 1. Случайная величина Х задана рядом распределения:

Найти Р(х<2),Р(х>4), Р(2 х 4), М(х),D(х).

Вычислить М(Y),D(Y) если Y=2X + 2.

Решение:

Р(х<2) = 0,1; Р(х>4) = 0,1; Р(2 х 4) = 0,2+0,4+0,2 = 0,8;

     М(х) = 1·0,1+2·0,2+3·0,4+4·0,2+5·0,1 = 3;

     D(х) = 1² ·0,1 + 2^{2 ·}0,2 + 3²·0,4 +4² ·0,2 + 5² ·0,1 - 3² = 1,2

     М(Y) = М(2Х + 2)= М(2Х)+ М(2)= 2· М(Х)+2 = 2·3 + 2 =8;

     D(Y) = D(2Х + 2)= D(2Х)+ D(2)= 4· D(Х)+0 = 4·1,2 = 4,8

Модой (М₀) называется значение случайной величины, которое встречается чаще всего, т.е. имеет максимальную вероятность ( для дискретной случайной величины).

Медианой (М_е) называется значение, которое делит область значений случайной величины на две равных по вероятности части.

4. Задачи математической статистики.

Назовем множество всех изучаемых однородных объектов генеральной совокупностью. Выборочной совокупностью  (или кратко выборкой) назовем объекты, отобранные для исследования из генеральной совокупности, а их число n объемом выборки. Назовем относительной частотой значения х_i частоту , где n_i – число повторения значений х_i в выборке объема n , х_i назовем вариантами. Соответствие между вариантами, записанными в порядке возрастания и относительными частотами, задаваемое таблицей статистического распределения выборки, называется статистическим (или эмпирическим) распределением выборки.